Units and Measurement Class 11 Physics Notes

The comparison of any physical quantity with its standard unit is called Measurement.

Physical Quantities

All the quantities which can be measured directly or indirectly in terms of which the laws of Physics are described are called physical quantities.

Units

A standard amount of a physical quantity chosen to measure the physical quantity of the same kind is called a physical unit. It should be easily reproducible, internationally accepted.

Fundamental Quantities and Their Units

Those physical quantities which are independent to each other are called fundamental quantities and their units are called fundamental units.

Fundamental Quantitites	Name	Symbol
Length	Metre	m
Mass	Kilogram	kg
Time	Second	s
Electric Current	Ampere	A
Thermodynamic temp.	Kelvin	K
Amount of substance	Mole	mol
Luminous intensity	Candela	cd

Supplementary Fundamental Quantities

Radian and steradian are two supplementary fundamental units. It measures plane angle and solid angle respectively.

Supplementary fundamental quantities	Name	Symbol
Plane angle	Radian	rad
Solid angle	Steradian	sr

Derived Quantities and Their Units

Those physical quantities which are derived from fundamental quantities are called derived quantities and their units are called derived units e.g. Velocity, acceleration, force, work etc.

System of Units

A system of units is the complete set of units, both fundamental and derived, for all kinds of physical quantities. The common system of units which is used in mechanics are given below:

1. CGS System: In this system, the unit of length is centimetre, the unit of mass is gram and the unit of time is second.
2. FPS System: In this system, the unit of length is foot, the unit of mass is pound and the unit of time is second.
3. MKS System: In this system, the unit of length is metre, the unit of mass is kilogram and the unit of time is second.
4. SI System: The system of units, which is accepted Internationally for measurement is the System Internationaled units abbreviated as SI. This system contains Seven fundamental units and two supplementary fundamental units.

Relationship between Some Mechanical SI Unit and Commonly Used Units

S.No	Physical Quantities	Unit
1.	Length	(a) 1 micrometre = 10-6 m (b) 1 nanometre = 10-9 m (c) 1 angstrom = 10-10 m
2.	Mass	(a) 1 metric ton = 103 kg (b) 1 pound = 0.4537 kg (c) 1 amu = 1.66 × 10-23 m
3.	Volume	1 litre = 10-3 m3
4.	Force	(a) 1 dyne = 10-5 N (b) 1kgf = 9.81 N
5.	Pressure	(a) 1 kgf-m2 = 9.81 Nm-2 (b) 1 mm of = 133 Nm-2 (c) 1 Pascal = 1 Nm-2 (d) 1 atmosphere pressure = 76 cm of Hg = 1.01 × 105 Pascal
6.	Work and Energy	(a) 1 erg = 10-7 J (b) 1kgf-m = 9.11 J (c) 1 kWh = 3.6 × 106 J (d) 1 eV = 1.6 × 10-19 J
7.	Power	(a) 1 kgf-ms-1 = 9.81 W (b) 1 horse power = 746 W

Some Practical Units of Length

1. 1 fermi = 10^-15 m
2. 1 X-ray Unit = 10^-13 m
3. 1 astronomical unit = 1.49 × 10¹¹ m
4. 1 light year = 9.46 × 10¹⁵ m
5. 1 parsec = 3.08 × 10¹⁶ m = 3.26 light year

Dimensions

Dimensions of any physical quantity are those powers to which the fundamental quantities are raised to express that quantity. The expression of a physical quantity in terms of its dimensions, is called its dimensional formula.

Dimensional Formula of Some Physical Quantities

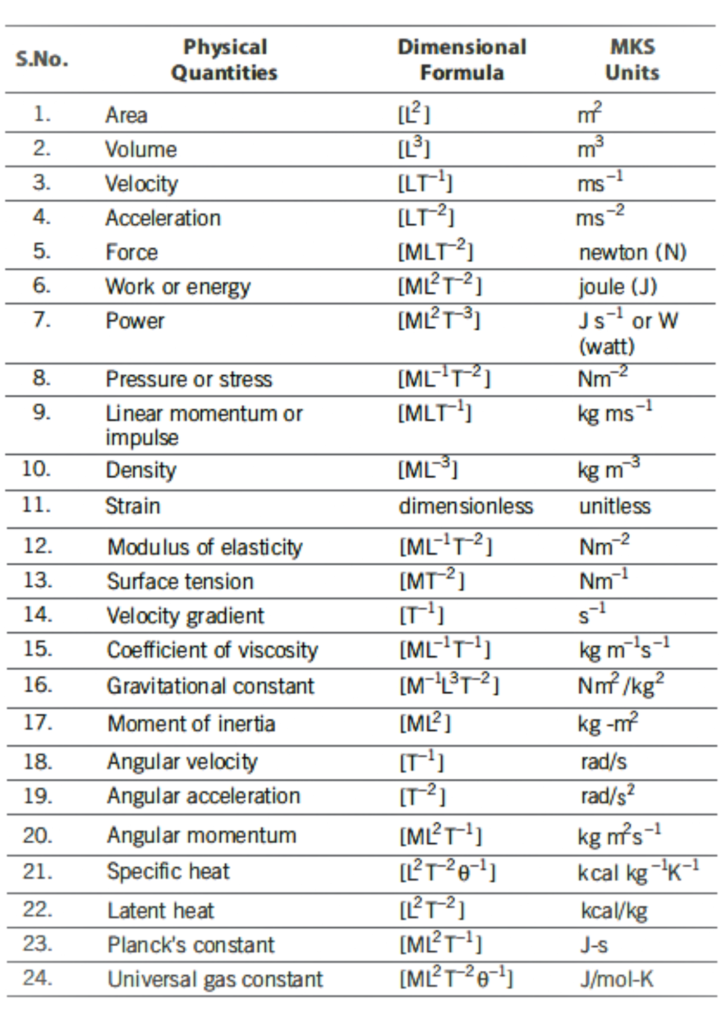
Homogeneity Principle

If the dimensions of left hand side of an equation are equal to thedimensions of right hand side of the equation, then the equation isdimensionally correct. This is known as homogeneity principle. Mathematically, [LHS] = [RHS].

Applications of Dimensions

1. To check the accuracy of physical equations.
2. To change a physical quantity from one system of units to another system of units.
3. To obtain a relation between different physical quantities.

Significant Figures

In the measured value of a physical quantity, the number of digits about the correctness of which we are sure plus the next doubtful digit, are called the significant figures.

Rules for Finding Significant Figures

1. All non-zeros digits are significant figures, e.g. 4362 m has 4 significant figures.
2. All zeros occuring between non-zero digits are significant figures, e.g. 1005 has 4 significant figures.
3. All zeros to the right of the last non-zero digit are not significant, e.g. 6250 has only 3 significant figures.
4. In a digit less than one, all zeros to the right of the decimal point and to the left of a non-zero digit are not significant, e.g. 0.00325 has only 3 significant figures.
5. All zeros to the right of a non-zero digit in the decimal part are significant, e.g. 1.4750 has 5 significant figures.

Significant Figures in Algebraic Operations

(1). In Addition or Subtraction: In addition or subtraction ofthe numerical values, the final result should retain as manydecimal places as there are in the number with the least places. e.g.

Rounding Off

The process of omitting the non significant digits and retaining only the desired number of significant-digits, incorporating the required modifications to the last significant digit is called rounding off the number.

Rules for Rounding Off a Measurement

1. If the digit to be dropped is less than 5, then the preceding digit is left unchanged. e.g. 1.54 is rounded off to 1.5.
2. If the digit to be dropped is greater than 5, then the preceding digit is raised by one. e.g. 2.49 is rounded off to 2.5.
3. If the digit to be dropped is 5 followed by digit other than zero, then the preceding digit is raised by one. e.g. 3.55 is rounded off to 3.6.
4. If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is raised by one, if it is odd and left unchanged if it is even. e.g. 3.750 is rounded off to 3.8 and 4.650 is rounded off to 4.6.

Error

The lack in accuracy in the measurement due to the limit of accuracy of the measuring instrument or due to any other cause is called an error. The difference between the measured value and the true value of a quantity is known as the error in the measurement.
Errors are usually classified as:

(1). Absolute Error

The difference between the true value and the measured value of a quantity is called absolute error. If a a a₁, a₂, a₃,…,a_n are the measured values of any quantity a in an experiment performed n times, then the arithmetic mean of these values is called the true value (a_m)

$$a_m=\frac{a_1+a_2+a_3+\dots+a_n}n$$

The absolute error in measured values is given by:

• Δa₁ = a_m– a₁
• Δa₂ = a_m– a₂
• Δa_n = a_m– a_n

The ratio of mean absolute error to the true value is called relative error.

$$Relative\;error\;=\;\frac{Mean\;absolute\;error}{True\;value}=\frac{\overline{\bigtriangleup a}}{a_m}$$

(4). Percentage Error

The relative error expressed in percentage is called percentage error.

$$Percentage\;error\;=\;\frac{\overline{\bigtriangleup a}}{a_m}\times100\%$$

Detailed Explanation With Video Lectures